Phân tích Ứng dụng giải BĐT, biện luận nghiệm là chủ đề trong bài viết hiện tại của blog Emerald City Convergence. Tham khảo bài viết để biết đầy đủ nhé.
Bài viết giúp các bạn hiểu rõ định nghĩa về tập giá trị hàm số và các ứng dụng trong việc giải bất đẳng thức, biện luận nghiệm của phương trình.
Định nghĩa về tập giá trị của hàm số
Phần này sẽ giúp bạn hiểu hơn về 3 định nghĩa về tập giá trị: Định nghĩa theo ánh xạ, định nghĩa theo hàm số và định nghĩa dựa vào tập xác định của hàm số.
Lưu ý: Link tải tài liệu được đặt ở cuối bài viết.

Tập giá trị của các hàm số cơ bản
Các hàm số cơ bản thường gặp: Hàm hằng, hàm số bậc nhất, hàm số bậc hai, hàm giá trị tuyệt đối.
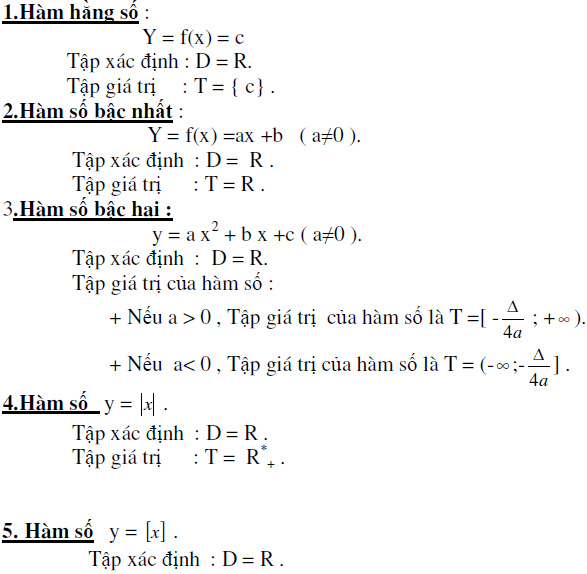
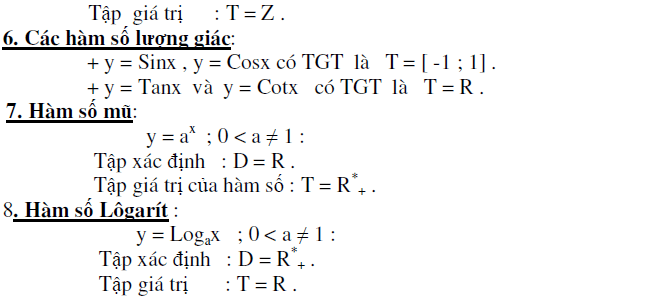
Phương pháp tìm tập giá trị hàm số
Phương pháp 1: Tìm tập xác định của hàm số ngược
Ta đã biết rằng hai hàm số ngược nhau thì tập giá trị của hàm số này là tập xác định của hàm số kia và ngược lại. Do đó, để tìm tập giá trị của một hàm số ta đi tìm tập xác định của hàm số ngược của nó.
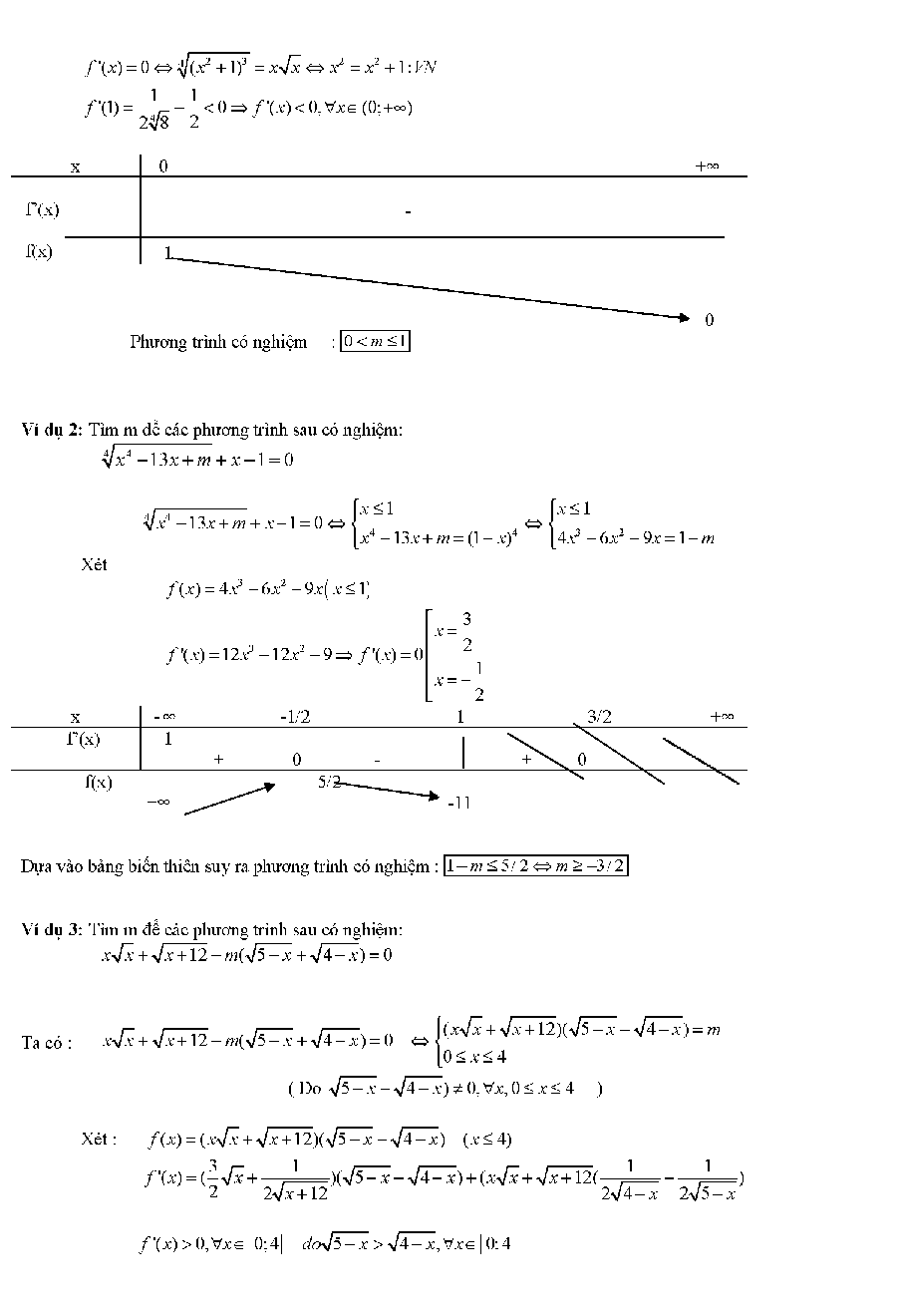
Ví dụ 1
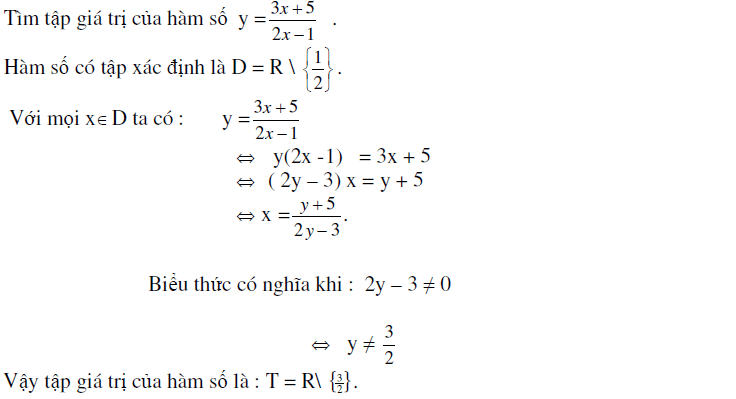
Áp dụng phương pháp trên chúng ta có thể tìm được tập giá trị của một số hàm số như sau:
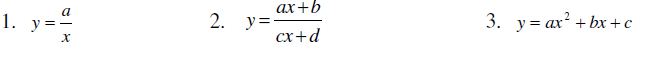
Phương pháp 2: Tìm tập giá trị của hàm số từ điều kiện có nghiệm của phương trình
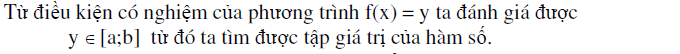
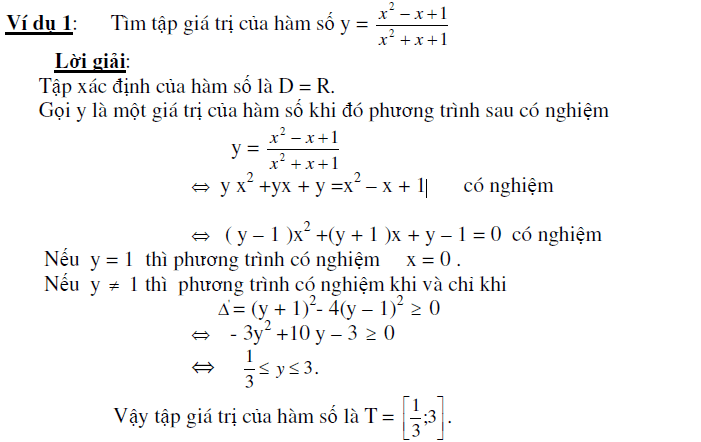
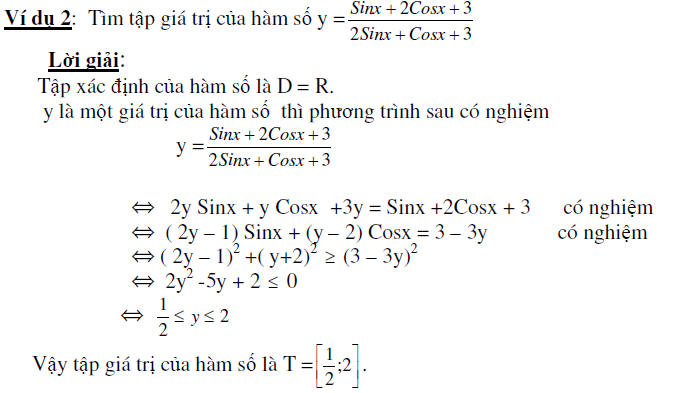
Phương pháp 3: Tìm tập giá trị bằng cách sử dụng BĐT
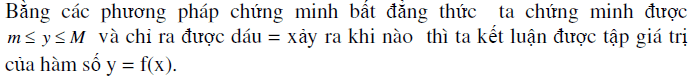
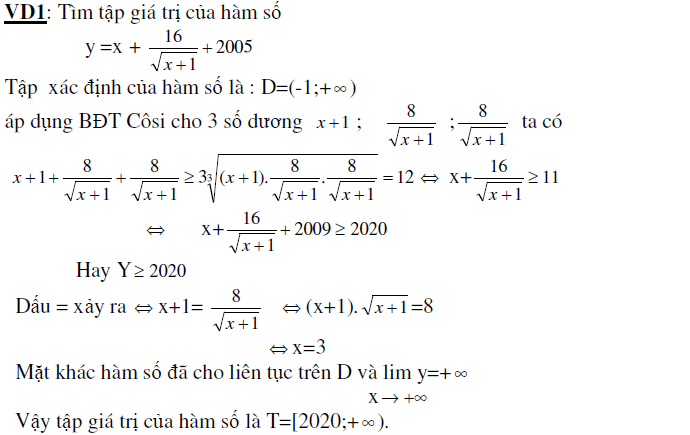
![]()
Phương pháp 3: Tìm tập giá trị hàm số bằng cách khảo sát hàm số
Bằng cách sử dụng đạo hàm để khảo sát hàm số, lập bảng biến thiên hàm số. Dựa vào bảng biến thiên chúng ta có thể kế luận về tập giá trị của hàm số.
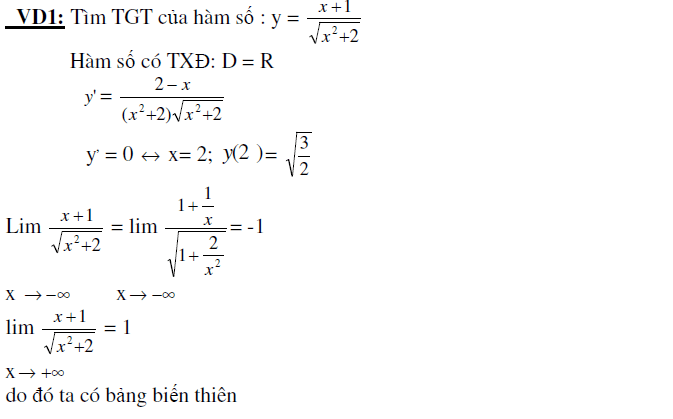
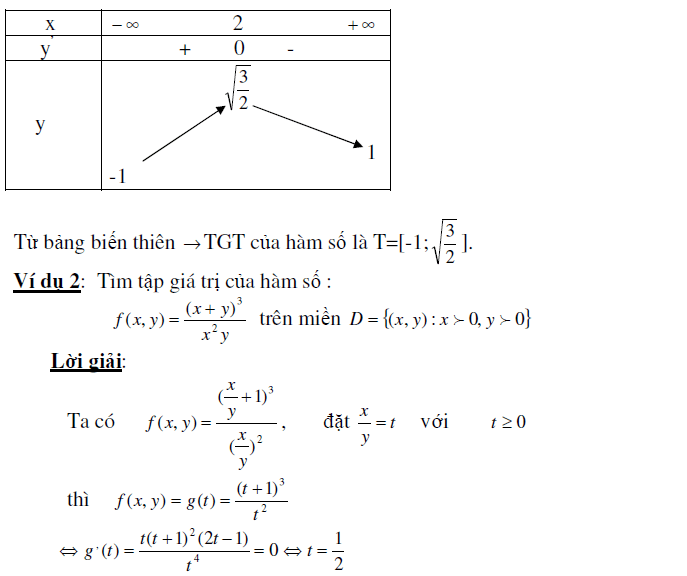
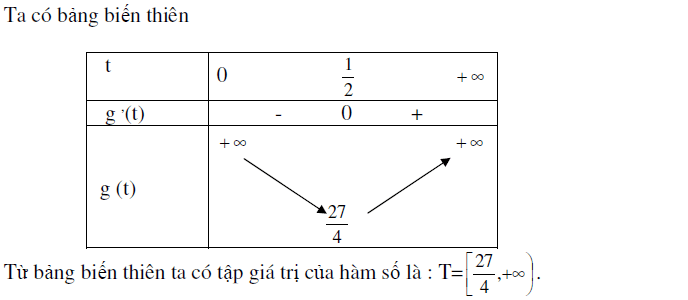
Nhận xét: Từ bảng biến thiên của hàm số chúng ta còn có thể kết luận được về GTLN, GTNN của hàm số đồng thời có thể biện luận được về số nghiệm của phương trình và giải được bất phương trình. Đó là những ứng dụng của tập giá trị hàm số mà chúng ta sẽ tìm hiểu ở các phần sau.
Một số bài tập nâng cao tìm tập giá trị
Để rèn luyện thêm các kỹ năng giải toán về tập giá trị cũng như các ứng dụng của nó chúng ta còn giải một số bài toán nâng cao như sau.




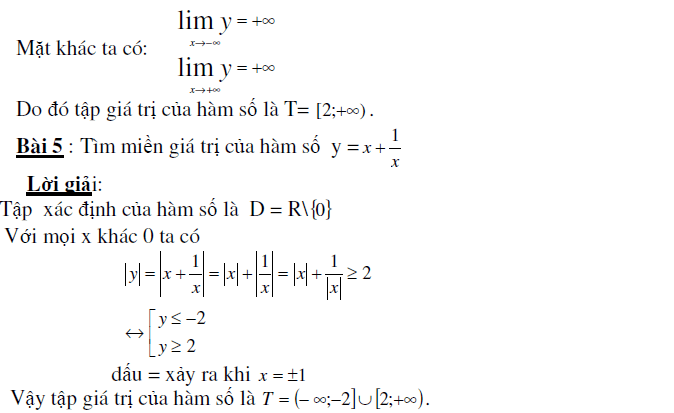
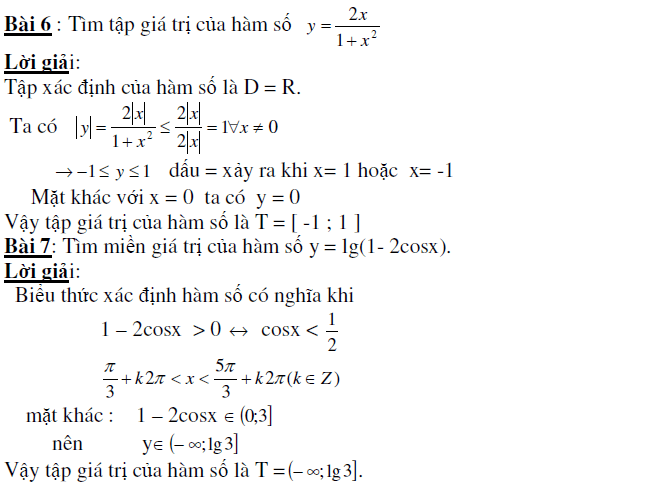
Ứng dụng của tập giá trị hàm số
Sử dụng các bài toán về tập giá trị của hàm số chúng ta đồng thời giải quyết được một số bài toán quan trọng thường gặp trong các kì thi tuyển sinh vào các trường ĐH – CĐ. Các bài toán có thể ứng dụng như: Chứng minh bất đẳng thức, tìm GTLN GTNN của hàm số, giải phương trình, giải bất phương trình.
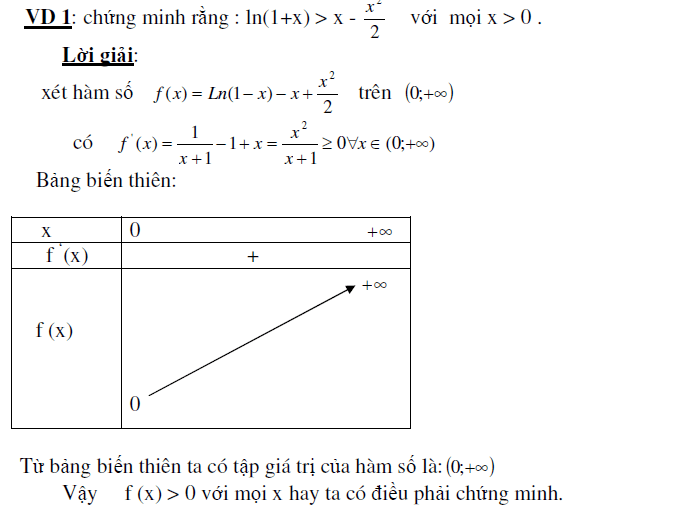
1. Ứng dụng giải bất đẳng thức
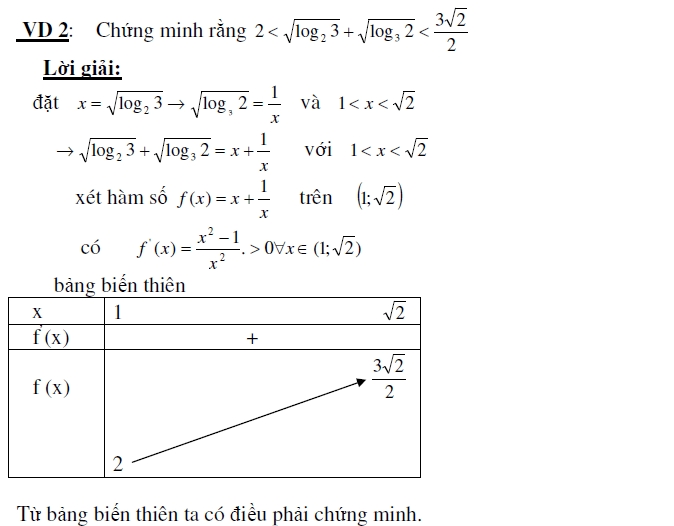
2. Tìm GTLN GTNN của hàm số

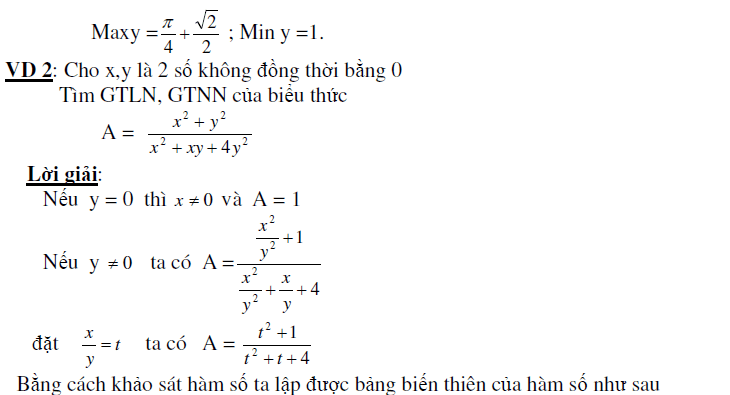
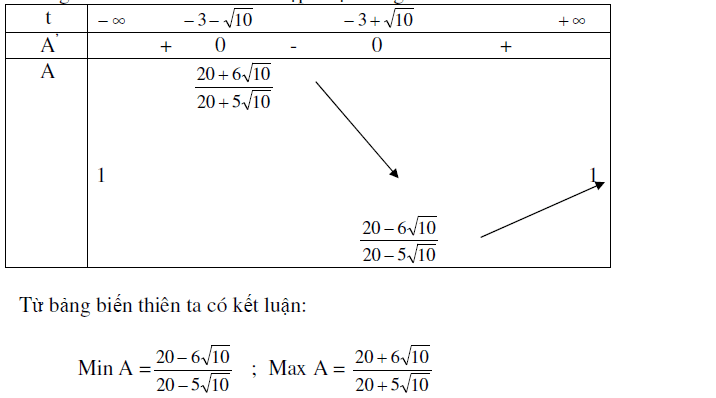
3. Ứng dụng vào giải phương trình
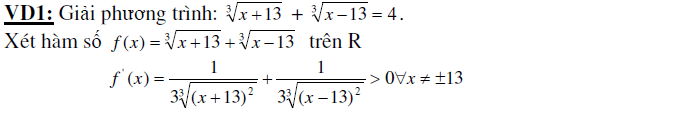

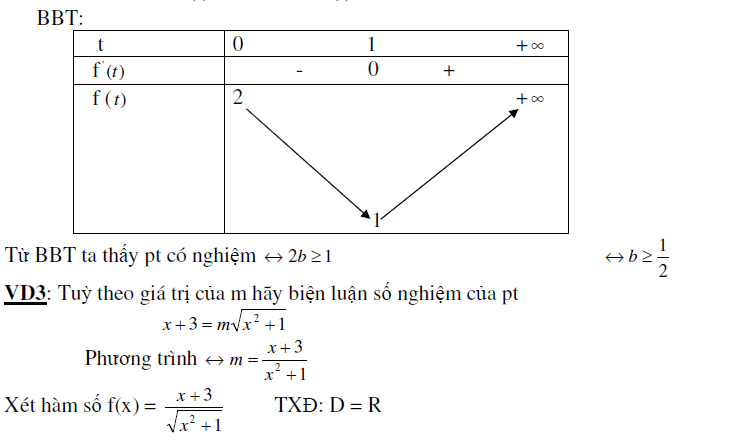

Ứng dụng đạo hàm tìm tập giá trị hàm số
Trong chương trình hiện nay, khi không còn sử dụng ĐL đảo về dấu tam thức bậc 2,khi giải các bài toán về biện luận số nghiệm của phương trình, bất phương trình, hệ phương trình ta thường hay gặp các bài toán liên quan đến
tham số. Có lẽ đây là dạng toán mà nhiều học sinh lúng túng nhất. Trong phần chúng ta sẽ xét một số dạng toán của phương trình vô tỉ mà chúng ta thương hay gặp (như xác định tham số để phương trình có nghiệm, có k nghiệm, nghiệm đúng với mọi x thuộc tập D nào đó… )